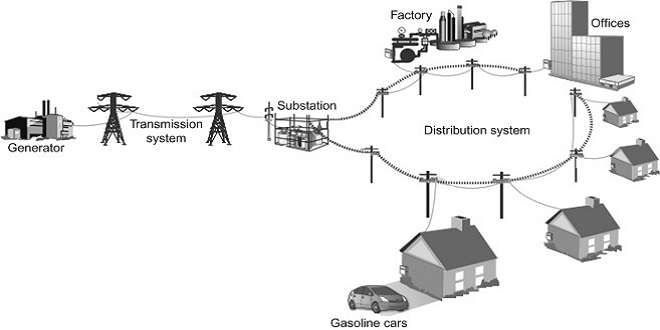
Thermodynamic Cycles: Potential and Limitations
The feasibility and limitations of thermodynamic cycles for the transformation of heat to work are considered in this chapter in relation to development scenarios for propulsion systems. These scenarios include thermal machines as direct propulsion systems, propulsion modules in hybrids, and onboard generators for electric energy. Thus, the efficiency of a thermal engine is considered in reference to its function as a propulsion system module, and not for a broad range of load and speed.
The transformation of heat to work in a thermal engine—if related to the quantity (obtained work) or to the quality (achieved thermal efficiency)—basically depends on the maximum and minimum temperature during heat input and heat release during the cycle. For a working fluid with known specific heat values at constant pressure and constant volume, the extreme temperatures of the available heat sources (warm source and cold source) are Tmax and Tmin (Kelvin). Considering the utilization of a thermal engine for automobile propulsion, the cold source is given by the ambient air. The warm source within a thermodynamic cycle is generated, in most cases, by combustion of a fuel and air mixture.
For comparable volumes of different types of thermal machines, the heat value of a fuel–air mixture Hu (kilojoules/kilogram mixture) is decisive, but not the heat value of the fuel itself, Hg (kilojoules/kilogram fuel). The mixture heat values for different fuels are. It should be noted that, despite the strong differences in heat values for different fuels, the mixture heat values for all kinds of fuel–air mixtures are more or less similar.
This fact is also determined by the strong differences between the stoichiometric air-to-fuel ratios for every fuel. The generation of a warm source by combustion of fuel with air is more efficient than any kind of heat transfer. On the other hand, the similar mixture heat values for gasoline, alcohol, oil, and hydrogen leads to the same domain of maximum temperature as a result of combustion.
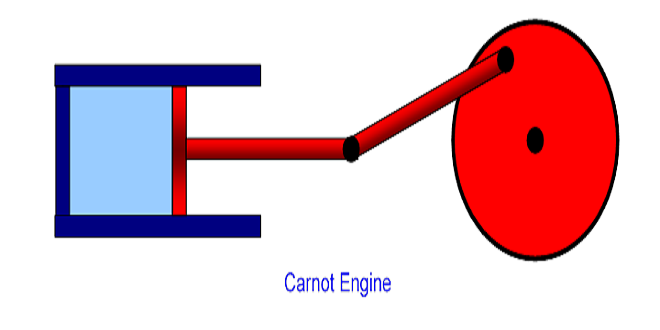
Carnot Cycle
The Carnot cycle has the advantage of the highest thermal efficiency between the considered temperature limits and thus of the minimum energy consumption for a considered cycle of work (when realizable). The Carnot cycle consists of two isothermic and two isentropic processes. The ideal cycle is represented in the pressure–volume–temperature (pVT). Independent of the heat transfer, this cycle is a chain of two compression and two expansion sequences (CDA and ABC).
Sterling Cycle
On the other hand, it should be mentioned that the heat input occurs in Stirling engines by heat transfer, whereas in gasoline and diesel engines there is direct combustion. This means that generally a lower speed is required in Stirling engines than in gasoline and diesel engines. However, this does not impair the power because the speed is compensated for by the value of the specific work.
Stirling engines with uniform heat transfer at low speed but remarkable work yield, at a swept volume and pressure and temperature values that are common for gasoline and diesel engines, could be very effective as on-board current generators for automobiles, as shown in Sect.
Otto Cycle
The Otto cycle consists of isochoric heat input and heat release and isentropic compression and expansion. Comparison of an ideal Otto cycle with other cycles at the same swept volume of 1.8 dm3 is based on a compression ratio of ε ¼ 12, which corresponds to current development tendencies for direct fuel injection. For these conditions, a working fluid mass (ideal air) of m ¼ 2.416 g was calculated. The extreme temperatures Tmax and Tmin have the same values as for the Carnot and Stirling cycles.
Last word
However, the speed of advanced gasoline engines is much higher than the speed of Sterling engines; therefore, the effective power at comparable swept volume is higher. The difference between four-stroke and two-stroke engines here is that the specific work is generated during two rotations or one, respectively.